In computer science, there are many cache algorithms in order to optimize the cache of information stored on the computer.

Normally, there is limited capacity for the cache allocated on the computer, and the computer needs to update the cache or delete the cache if the cache is full. There are many common algorithms for optimizing cache on a computer like: FIFO (First in first out), LFU (Least frequently used), LRU (Least recently used).

Today we are focusing on implementing the LRU (Least recently used) cache algorithm.

I will be using this problem 146. LRU Cache from LeetCode as the guideline for the implementation. Basically, we need to implement the following class:

1
2
3
4
5
6
7
8
9
10
11
12
13
class LRUCache:

    def __init__(self, capacity: int):

    def get(self, key: int) -> int:

    def put(self, key: int, value: int) -> None:


# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

Analyze

A rough thought is that we need to maintain a list-like data structure to store the cache sequentially, and update the list accordingly after each get or put operation.

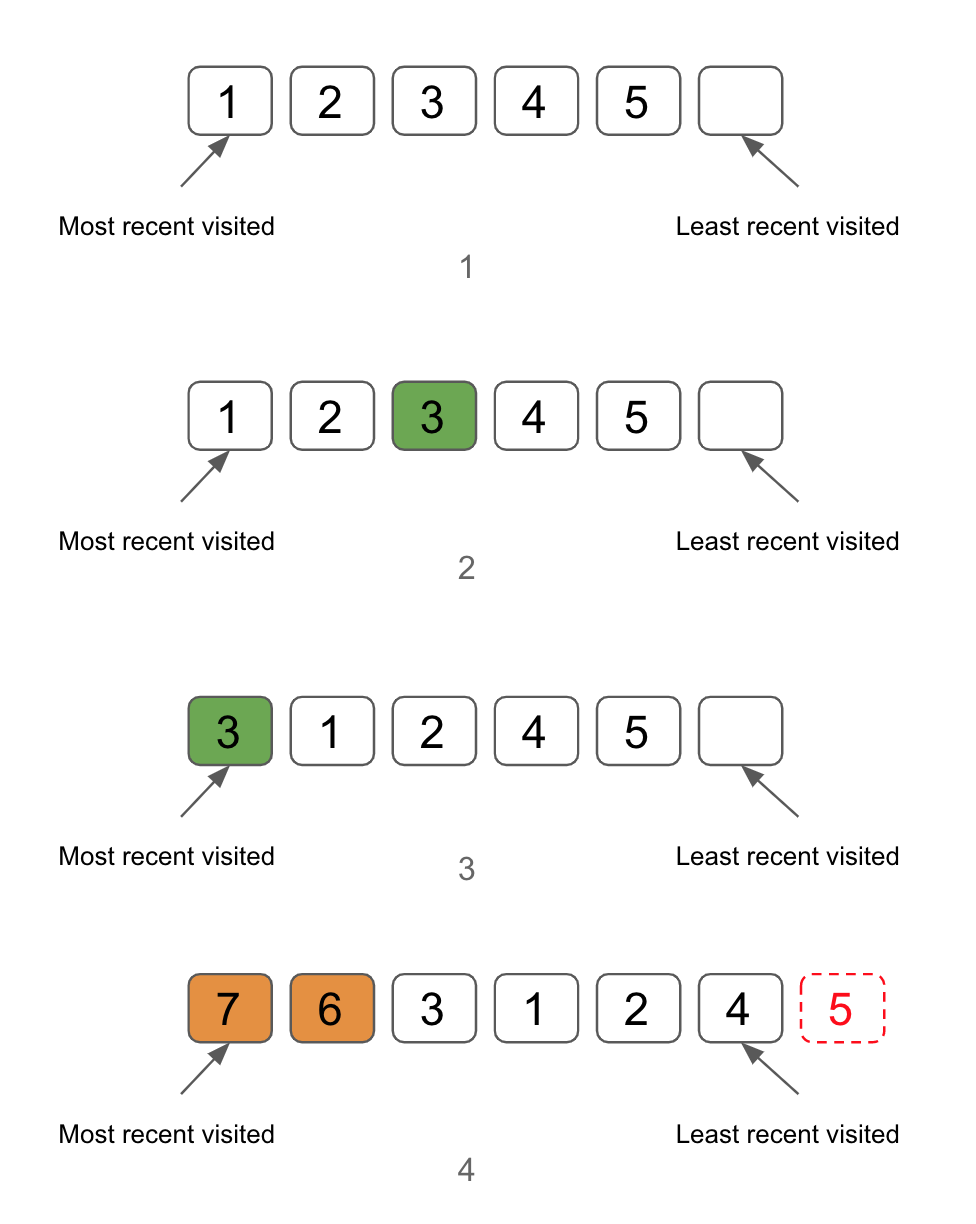
The data towards the end of the list is visited earlier and the data at the beginning is the most recent visited one.

Here is a list represents the cache. It has the capacity of 6, in which 5 of them are filled with data(1).

  • If 3 got visited(2), it will be moved to the beginning of the list(3).

  • If we put 6 and 7 into the cache, 5 will be moved out of the cache since it reaches the capacity of the cache(4).

LRU

Using Array

Using an array is pretty straightforward. We have defined a few properties to the class:

  • cacheData: a dictionary to store the key and value
  • cacheKey: an array to store only the keys in a specific order
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class LRUCache_Array:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cacheData = {}
        self.cacheKey = []

    def get(self, key: int) -> int:
        if key in self.cacheData.keys():
        # check if the data already in the cache
            if key in self.cacheKey:
                # remove the key from cacheKey
                self.cacheKey.remove(key)
            # add the key back to cacheKey at the begining of the array since it is visited
            self.cacheKey = [key] + self.cacheKey
            # return the value of the data from the cacheData dictionary
            return self.cacheData[key]
        return -1

    def put(self, key: int, value: int) -> None:
        if key in self.cacheData.keys():
            # if key already in the cacheData, update the value of the data
            self.cacheData[key] = value
            # move the key from cacheKey to the beginning of the array
            if key in self.cacheKey:
                self.cacheKey.remove(key)
            self.cacheKey = [key] + self.cacheKey
        else:
            # if the key not in cacheData yet, we need to check if the cacheData exceeds the capacity first before we put the data into the cache
            if len(self.cacheData) < self.capacity:
                # add the data to cacheData, and insert the key at the beginning of the cacheKey array if there is still room
                self.cacheData[key] = value
                self.cacheKey = [key] + self.cacheKey
            else:
                # if exceeds the capacity, remove the last key from cacheKey and delete the data from cacheData.
                lastDataKey = self.cacheKey.pop()
                del self.cacheData[lastDataKey]
                # then insert the data and the key
                self.cacheData[key] = value
                self.cacheKey = [key] + self.cacheKey

Since we are manipulating the key in an array, for example remove or concatenation, the time complexity of those operations is O(n). And the lookup time on a dictionary in Python is O(1). So the time complexity of each operation(get and put) in this implementation will be O(n).

Using Doubly Linked List

For the doubly linked list, we will need to define an extra ListNode class, which has prev and next pointing to its previous node and next node respectively.

1
2
3
4
5
6
7
# define the double linked-list node
class ListNode:
    def __init__(self, key = None, value = None):
        self.key = key
        self.value = value
        self.next = None
        self.prev = None

Then we will need to define a few properties in our implementation:

  • cacheData: a dictionary to store the key and value
  • head: a head node pointing to the first node of the linked list, initialized as None
  • tail: a tail node pointing to the last node of the linked list, initialized as None
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
# Used double linked-list to maintain the node. O(1)
class LRUCache_LinkedList:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cacheData = {}
        self.head: ListNode = None
        self.tail: ListNode = None

    def get(self, key: int) -> int:
        node = self.cacheData.get(key)
        if node:
            # move the current node to the front of the linked list
            self.__moveNodeToFront(node)
            return node.value
        return -1

    def put(self, key: int, value: int) -> None:
        node = self.cacheData.get(key)
        if node:
            # key already exsit in cache, update the value
            node.value = value
            # move the node to front since it has been updated
            self.__moveNodeToFront(node)
        else:
            newNode = ListNode(key, value)
            self.cacheData[key] = newNode
            self.__addNodeAtFront(newNode)
            if len(self.cacheData) > self.capacity:
                del self.cacheData[self.tail.key]
                self.__removeNode(self.tail)

    def __moveNodeToFront(self, node: ListNode):
        self.__removeNode(node)
        self.__addNodeAtFront(node)

    def __removeNode(self, node: ListNode):
        # This method needs to consider if the node you want to remove is the head or the tail.
        n = node.next # if node is tail, then n will be None
        p = node.prev # if node is head, then p will be None
        if not p:
            self.head = n
            node.next = None
            if n:
                n.prev = None
        else:
            p.next = n
            if n:
                n.prev = node.prev
            else:
                self.tail = node.prev
                node.prev = None

    def __addNodeAtFront(self, node: ListNode):
        if not self.head:
            # if the linked list does not exist yet
            self.head = node
            self.tail = node
            return
        node.next = self.head  
        self.head.prev = node
        node.prev = None
        self.head = node

Since the time complexity of insertion or deletion operation on a doubly linked list is O(1), and the lookup time on a dictionary in Python is O(1). So the time complexity of each operation(get and put) in this implementation will be O(1).